martes, 13 de noviembre de 2012
lunes, 12 de noviembre de 2012
1. Sistemas de ecuaciones lineales
Cuando nos planteamos la resolución de varias ecuaciones a la vez con varias incógnitas, estamos ante un sistema y en el caso más sencillo, donde todas las ecuaciones sean lineales, se llama sistema de ecuaciones lineales.
Existen muchas formas de resolver dichos sistemas, empezando por las
clásicas de reducción, sustitución e igualación. Ahora bien, dado un sistema no
siempre es necesario resolverlo sino que, a veces, sólo hace falta saber si
tiene o no solución: En cuanto a la resolución de dichas ecuaciones daremos
algunos sencillos métodos y utilizaremos el método de Gauss como otra
alternativa de resolución.
Definición.
Se llama sistema de ecuaciones lineales a un conjunto de ecuaciones de
la forma:
Matriz de coeficientes
|
- Donde x1, ..., xn son las
incógnitas.
- b1, ..., bm se denominan
términos independientes.
- Los números aij se llaman
coeficientes de las incógnitas.
Sistemas Homogéneos:
Un sistema homogéneo es aquel que tiene todos los términos
independientes nulos.
Cualquier sistema homogéneo es evidente que es compatible,
pues dando a cada incógnita el valor 0, se cumplen las ecuaciones. Esta solución
(que todas las incógnitas sean nulas) se llama solución trivial.Cuando el término independiente sea cero, estamos ante un caso particular de sistemas que denominamos homogéneos, es decir:
Un conjunto de n números que verifiquen todas las ecuaciones se llama
solución del sistema. Dado un sistema de ecuaciones, el objetivo principal es
hallar todas sus soluciones, es decir, hallar todos los valores de x1, ..., xn
que verifican todas las ecuaciones.
Ecuación Pendiente
La pendiente m de una recta que pasa por los puntos (x1 ,
y1) y (x2 , y2) está dada por :
Ecuación punto pendiente:
También es posible hallar la ecuación de una recta con tan sólo tener su
pendiente y uno de los puntos, con la siguiente relación:
y – y1 = m
(x – x1)
Cualquier recta (excepto una con pendiente indefinida) se
puede escribir en la forma pendiente –
ordenada
y = mx + b
Donde m es la
pendiente y b es la ordenada al origen.
Pendiente indefinida:
Si x2 – x1 = 0 y y2 diferente a
y1, la línea recta es vertical y se dice que su pendiente es indefinida.
Dos recta distintas son paralelas si y sólo si tienen la
misma pendiente.
Si m1 es la pendiente de la recta L1, m2 es la pendiente de
la recta L2, m1 diferente de cero y L1 y L2 son
perpendiculares, entonces:
Las rectas paralelas al eje x tienen una pendiente de cero.
FORMA GENERAL DE LOS SISTEMAS DE ECUACIONES
Dos ecuaciones con dos incógnitas:
a21 x + a22 y = b2
Donde a11 , a12, a21, a22 se denominan coeficientes de las
variables.
Atendiendo al número de soluciones, los sistemas de
ecuaciones lineales podemos clarificarlos en tres tipos:
Sistema incompatible: Son aquellos que no poseen solución.
x – y = 7 y 2x –
2y = 13
Sistema compatible: Son aquellos que poseen solución. Dentro
de ellos, podemos hablar de:
Sistema compatible determinado: Sistemas con una única
solución.
x – y = 7 y x + y = 5
Sistema compatible indeterminado: Sistemas con infinitas
soluciones.
x – y = 7 y 2x – 2y = 14
Su representación gráfica es:
STANLEY I, Grossman. Algebra Lineal. Mc
Graw
Hill. México 2000.
TAHA, Hamdy A.
Investigación de Operaciones una
introducción. 5 ed. México. D.F.:Alfaomega 2004.
2. Método eliminación Gauss - Jordan
1. Determine la primer columna (a la izquierda) no cero.
2. Si el primer elemento de la columna es cero,
intercámbielo por un renglón que no tenga cero.
3. Obtenga ceros abajo del elemento delantero sumando múltiplos adecuados a los renglones debajo de el.
4. Cubra el renglón y la columna de trabajo y repita el
proceso comenzando en el paso 1. Al termino del ciclo entre el paso 1 al 4
(es decir cuando se han barrido todos los renglones), la matriz deber a
tener forma de escalón.
5. Comenzando con el ultimo renglón no cero avance
hacia arriba para que en cada renglón tenga un 1 delantero y arriba de
el queden solo ceros. Para ello deber a sumar múltiplos adecuados del renglón a los renglones correspondientes.
Es importante observar que en el método de
eliminación Gaussiana:
- Los pasos del 1 a 4 aplicados repetidamente escalonan la matriz; el paso 5 aplicado repetidamente reduce la matriz.
- En el paso 2, si el elemento no es cero no se realiza intercambio.
- En el paso 3, los elementos que se hacen cero son solo los inferiores al pivote
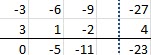
Hallar Pivote
Nueva F2
Nueva F3
.bmp)
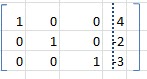
Hallar Pivote
.bmp)
3. Matriz de Leontieff
EL PROBLEMA ECONOMICO DE LAS RELACIONES ÍNTER-INDUSTRIALES
El análisis de cuadros de insumo-producto, fue desarrollado
por W.W. Leontief en 1936, como el instrumento de interpretación de las
interdependencias de los diversos sectores de la economía. Es decir, en el análisis
de insumo-producto consideramos cualquier sistema económico como un complejo de
industrias mutuamente interrelacionadas. Se considera que toda industria recibe
materias primas (insumos) de las demás industrias del sistema y que, a su vez,
proporciona su producción a las demás industrias en calidad de materia prima. Fundamentalmente
se trata de un análisis general del equilibrio estático de las condiciones tecnológicas
de la producción total de una economía, durante el periodo de tiempo en cuestión.
La Matriz de Transacciones Ínter-industriales
A grandes rasgos, la economía en su conjunto se divide en el
sector productor y en el sector consumidor; el sector productor, a su vez se
divide en un gran número de industrias en el cual se supone que cada industria produce
un producto homogéneo.
El punto de partida para la elaboración de un análisis de
insumo-producto es la formulación de una tabla que contiene partidas que
demuestran, ya sea cuantitativamente o en términos de valor, de qué manera se
distribuye la producción total de una industria a todas las demás industrias en
forma de producción intermedia (es decir, como materia prima) y a los usuarios
finales no productores.
Esta es una tabla de transacciones ínter-sectoriales, que
muestran como se ínter-relacionan todas las industrias, en el sentido de que
cada una adquiere productos fabricados por las demás a fin de llevar a cabo su
propio proceso.
Los sectores de esta tabla son precisamente Agricultura,
Industria y Servicios. Estos nombres reflejan un concepto amplio, en el sentido
de que dentro del sector servicios se agrupan todas las empresas que prestan algún
tipo de servicio, tales como: bancos, transporte de carga, transporte de
pasajeros, comercios, servicios profesionales diversos, servicios públicos
diversos, etc. Dentro del sector industrial se agrupan todas las empresas que
producen bienes, tales como: industria textil, farmacéutica, petroquímica, de energéticos,
de alimentos, de bebidas, de plástico, de papel y derivados, etc. En el sector agricultura
se agrupan todas las empresas agrícolas y ganaderas de diversos tipos, tales como:
producción de hortalizas, de cereales, de forrajes, de ganado lechero, de
ganado lanar, avícola, porcino, etc., o según otra clasificación más
conveniente.
CALCULAR
MATRIZ
Se continua con el método Gauss Jordán
4. Asignación de recursos
La asignación de recursos es la distribución de activos
productivos en sus diferentes usos.
El asunto de la asignación de recursos, se origina de como
las organizaciones buscan balancear los recursos limitados como el capital, el
trabajo y la tierra, frente a las diversas e ilimitadas necesidades de sus
integrantes. Los mecanismos de asignación de recursos abarcan el sistema de
precios en las economías de libre mercado.
La finalidad de distribuir los recursos es siempre la de
obtener la máxima productividad posible a partir de una combinación dada de
activos. Por consiguiente los mecanismos de asignación mas conocidos son las
empresas, el hogar y el gobierno
Video:
Ejemplo:
Asignación de recursos en las lineas de producción de fritolay, donde si asignan los diferentes productos a las distintas freidoras dependiendo la cantidad de producto y la capacidad de las maquinas.
5. Vectores y matrices
El vector es una matriz que tiene únicamente un renglón o
una columna.
Vector renglón: Es una matriz que tiene un solo renglón. Un
vector renglón de "n" componentes, conjunto ordenado de n números escritos así:
(X1 X2 X3… Xn) = ( 7, 3, 5 )
Vector columna: Es una matriz que tiene una columna solamente. Un vector columna de "n" elementos, conjunto ordenado de n números escritos así:
MATRICES
Una matriz es un
arreglo rectangular de números dispuestos en filas y columnas y encerrados
entre corchetes o paréntesis. Para representar a una matriz se utilizan letras
mayúsculas. El orden de una matriz se representa como: m x n, donde “m” es el
número de filas y “n” el número de columnas.
Ejemplo:
Representación
general de una matriz de orden m x n
Donde:
aij: Es el
elemento o entrada general ubicado en la fila “i” , columna j
Matriz fila o vector fila: Ejm:/ B= ( 3 -2 5 6 ) 1 X 4
Matriz columna o vector columna:
Ejm:/
6. Igualdad de matrices
Ejemplos,
|1 2 3| es igual a |1 2 6/2|.
Suscribirse a:
Comentarios (Atom)





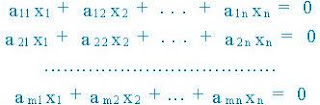




.bmp)
.bmp)
.bmp)
.bmp)
++de+Nueva+imagen+(4).bmp)
.bmp)
++de+Nueva+imagen+(5).bmp)
++de+Nueva+imagen+(5).bmp)
.bmp)
.bmp)
.bmp)
.bmp)
.bmp)





.bmp)



.bmp)
.bmp)
.bmp)