1. Determine la primer columna (a la izquierda) no cero.
2. Si el primer elemento de la columna es cero,
intercámbielo por un renglón que no tenga cero.
3. Obtenga ceros abajo del elemento delantero sumando múltiplos adecuados a los renglones debajo de el.
4. Cubra el renglón y la columna de trabajo y repita el
proceso comenzando en el paso 1. Al termino del ciclo entre el paso 1 al 4
(es decir cuando se han barrido todos los renglones), la matriz deber a
tener forma de escalón.
5. Comenzando con el ultimo renglón no cero avance
hacia arriba para que en cada renglón tenga un 1 delantero y arriba de
el queden solo ceros. Para ello deber a sumar múltiplos adecuados del renglón a los renglones correspondientes.
Es importante observar que en el método de
eliminación Gaussiana:
- Los pasos del 1 a 4 aplicados repetidamente escalonan la matriz; el paso 5 aplicado repetidamente reduce la matriz.
- En el paso 2, si el elemento no es cero no se realiza intercambio.
- En el paso 3, los elementos que se hacen cero son solo los inferiores al pivote
Hallar Pivote
Nueva F2
Nueva F3
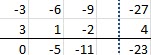.bmp)
Hallar Pivote
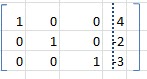.bmp)


.bmp)
.bmp)
.bmp)
.bmp)
++de+Nueva+imagen+(4).bmp)
.bmp)
++de+Nueva+imagen+(5).bmp)
++de+Nueva+imagen+(5).bmp)
.bmp)
.bmp)
.bmp)
.bmp)
.bmp)
No hay comentarios:
Publicar un comentario