Cuando nos planteamos la resolución de varias ecuaciones a la vez con varias incógnitas, estamos ante un sistema y en el caso más sencillo, donde todas las ecuaciones sean lineales, se llama sistema de ecuaciones lineales.
Existen muchas formas de resolver dichos sistemas, empezando por las
clásicas de reducción, sustitución e igualación. Ahora bien, dado un sistema no
siempre es necesario resolverlo sino que, a veces, sólo hace falta saber si
tiene o no solución: En cuanto a la resolución de dichas ecuaciones daremos
algunos sencillos métodos y utilizaremos el método de Gauss como otra
alternativa de resolución.
Definición.
Se llama sistema de ecuaciones lineales a un conjunto de ecuaciones de
la forma:
Matriz de coeficientes
|
- Donde x1, ..., xn son las
incógnitas.
- b1, ..., bm se denominan
términos independientes.
- Los números aij se llaman
coeficientes de las incógnitas.
Sistemas Homogéneos:
Un sistema homogéneo es aquel que tiene todos los términos
independientes nulos.
Cualquier sistema homogéneo es evidente que es compatible,
pues dando a cada incógnita el valor 0, se cumplen las ecuaciones. Esta solución
(que todas las incógnitas sean nulas) se llama solución trivial.Cuando el término independiente sea cero, estamos ante un caso particular de sistemas que denominamos homogéneos, es decir:
Un conjunto de n números que verifiquen todas las ecuaciones se llama
solución del sistema. Dado un sistema de ecuaciones, el objetivo principal es
hallar todas sus soluciones, es decir, hallar todos los valores de x1, ..., xn
que verifican todas las ecuaciones.
Ecuación Pendiente
La pendiente m de una recta que pasa por los puntos (x1 ,
y1) y (x2 , y2) está dada por :
Ecuación punto pendiente:
También es posible hallar la ecuación de una recta con tan sólo tener su
pendiente y uno de los puntos, con la siguiente relación:
y – y1 = m
(x – x1)
Cualquier recta (excepto una con pendiente indefinida) se
puede escribir en la forma pendiente –
ordenada
y = mx + b
Donde m es la
pendiente y b es la ordenada al origen.
Pendiente indefinida:
Si x2 – x1 = 0 y y2 diferente a
y1, la línea recta es vertical y se dice que su pendiente es indefinida.
Dos recta distintas son paralelas si y sólo si tienen la
misma pendiente.
Si m1 es la pendiente de la recta L1, m2 es la pendiente de
la recta L2, m1 diferente de cero y L1 y L2 son
perpendiculares, entonces:
Las rectas paralelas al eje x tienen una pendiente de cero.
FORMA GENERAL DE LOS SISTEMAS DE ECUACIONES
Dos ecuaciones con dos incógnitas:
a21 x + a22 y = b2
Donde a11 , a12, a21, a22 se denominan coeficientes de las
variables.
Atendiendo al número de soluciones, los sistemas de
ecuaciones lineales podemos clarificarlos en tres tipos:
Sistema incompatible: Son aquellos que no poseen solución.
x – y = 7 y 2x –
2y = 13
Sistema compatible: Son aquellos que poseen solución. Dentro
de ellos, podemos hablar de:
Sistema compatible determinado: Sistemas con una única
solución.
x – y = 7 y x + y = 5
Sistema compatible indeterminado: Sistemas con infinitas
soluciones.
x – y = 7 y 2x – 2y = 14
Su representación gráfica es:
STANLEY I, Grossman. Algebra Lineal. Mc
Graw
Hill. México 2000.
TAHA, Hamdy A.
Investigación de Operaciones una
introducción. 5 ed. México. D.F.:Alfaomega 2004.



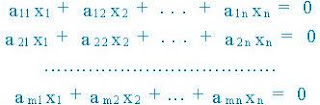




No hay comentarios:
Publicar un comentario